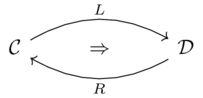
For any \(c \in C\) and \(d \in D\), there is an isomorphism of hom-sets: \(\alpha_{c,d}: \mathcal{C}(c,R(d)) \xrightarrow{\cong} \mathcal{D}(L(c),d)\) that is natural in c and d.
Given a morphism \(c \rightarrow{f} R(d)\) in \(\mathcal{C}\), its image \(g:=\alpha_{c,d}(f)\) is called its mate (and vice-versa)
To denote the adjunction we write \(L \dashv R\) or